大気減光の光路長の球体近似式を考てみた

大気減光の光路長とは？

夕日の写真や天体写真を撮るとき、光が大気の層を通過することによる減光が起きます。大気減光は、大気を構成する空気分子や大気中のエアロゾルによって起き、光の波長に依存します。しかし、最大の要因は仰角です。仰角が小さいほど（天体が地平線に近いほど）光路長が伸びるので、減光も光路長に比例して大きくなります。夕日がまぶしくないのはこのためです。

天文学では多くの場合、天頂からの光の光路長を1としたとき、天頂角（仰角の余角）z の天体の光路長を、1 / cos z とする近似式を用います。この近似式は、地表と大気層上面を、互いに平行な平面と考えたモデルを使っています。つまり、仰角 0（天頂角 90度） では、光路長は無限大になってしまい、夕日などには使えません。なのでこの式には必ず、天頂角 60度以内という、ただし書きが付いています。

夕日など仰角の小さい場合にも適用させるためには、地球を球体としたモデルを使う必要があります。しかし、ネットでざっと調べた限り、球体モデルの近似式を見つけることはできませんでした。そこで、自分で考えてみることにしました。

球体近似式のモデル

モデルの前提条件として、実際には回転楕円体である地球を、半径 r の球体と見なしました。大気は地表で 1 気圧、標高 5.5 km で 0.5 気圧、100 km あたりでほぼ真空、つまり宇宙になるわけですが、このような密度のグラデーションを式にするのは私の力量では無理なので、厚さ t の均等な層と仮定しました。また、大気の屈折率は 1.00028 と、わずかに真空より高いので、光が大気層に入射するときに屈折が起き、大気差という仰角のズレを起こすのですが、これは無視しました。

解法

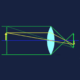
地表の観測者を A とし、仰角 α で見上げたとき、B で大気層が終わって宇宙になるとしました。そのときの辺ABの長さを、r、t、α から求めれば光路長が得られます。

角度として仰角 α だけを使うのは無理がありそうだったので、中心角 θ も使うことにして、いったん θ を r、t、α の式で表してから、最後に、その式を θ に代入するという解法をとりました。θ （実際には sin θ）を表す式は、三角関数が入って長くはなっていますが、単なる2次方程式になったので解くことができました。

以下が解法ですが、数式をテキスト入力するのは面倒なので、手書きの画像でお許しください。

計算結果

得られた球体近似式を Excel に入力して、r、t の定数を決め、最後にα の値を様々に変えて表にしました。

地球の半径 r の値は有効数字3桁程度で 6380 km にしました。t については、5.5 km で半分の気圧になることから、とりあえず 11 km にしました。

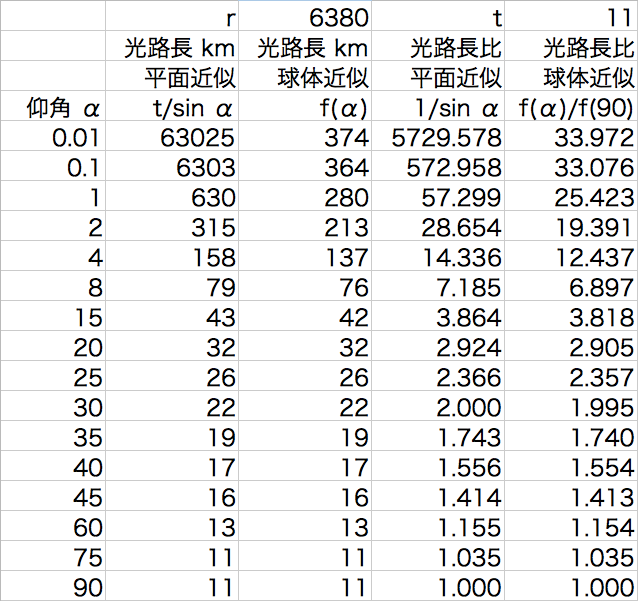
左カラムが仰角 α、2番目が平面モデル近似式による光路長、3番目が今回の球体モデル近似式による光路長です。4番目と5番目は、それぞれ天頂を1とした比です。

確かに仰角 30度以上では両者にほとんど差はありませんが、仰角 1度（太陽や月の視直径の約 2倍）では 2倍以上の値になっています。ただし、仰角 0度付近では、大気差が 0.5度くらいあると言われていますので、球面近似式の値を見るときも注意が必要です。

今後は、この光路長から求めた減光率と、実際に色々な仰角で撮った月の写真の輝度とを比べることで、どのくらい近似できているか調べてみようと考えています。

てことで、ではまた！

　　関連記事:

iPhone・iPad 用の Excel・Word・パワポが無料で配信開始！