たけしのコマ大数学科のアブー・アルワファー問題のもう一つの解法

 
こんばんは、数学大好き Iwasaki です。
 

テレビ番組「たけしのコマ大数学科」が終わっちゃいましたね、残念！
途中から見始めて、最後の 7、8 回は見ました。
毎回録画して、最初に問題だけ見て、自力で解いてから模範解答を見てました。最近、数学センスの衰えが気になってたので、ちょうどいい頭の体操でした。

で、今日の話題は、最終回前の 2013/9/17 放送分のアブー・アルワファー問題。

一辺の長さが a の正方形が 3 つあります。
これらをハサミで切って、組み合わせて 1 つの正方形を作りなさい。
ただし、切り刻んだ正方形の破片は余らないものとします。

とっかかりは簡単です。
出来上がった正方形の面積が、a 二乗の 3 倍ですので、一辺は √3 a になります。

記述が面倒くさいので、a = 1 にしちゃいましょう。
そうすると、一辺が √3 の正方形をどうにかして作ればいいことになります。

そんなに難しくもなさそう…
てことで、私は 30 分くらいで、ある解答に至りました。

ところが、番組の模範解答を見てみると、私のとは全く違った解法でした。

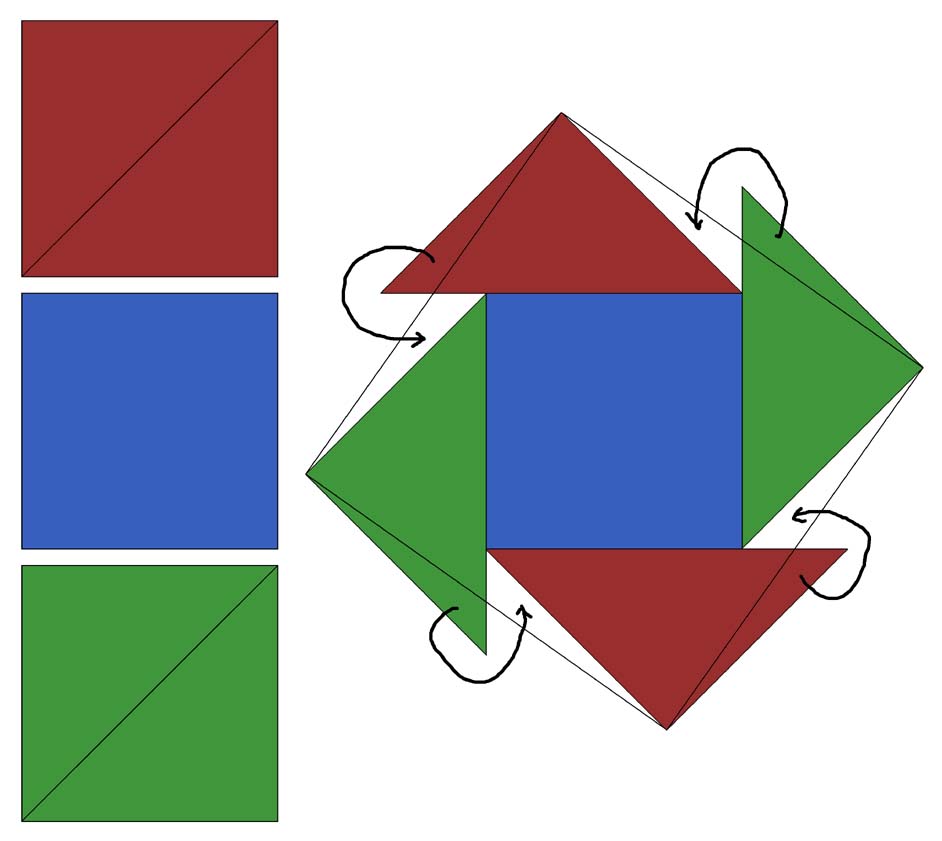
↓ その解法はこちら

↓

↓

実際、折り紙を切って試行錯誤してたら、マス（たけし）チームと同様、この解答にたどり着きそうですが、図形的には美しくても数学的にはどうも美しいとは感じられません。

なぜなら、一辺が √3 になることを直感的に理解しにくいからです。
（もちろん、こねくり回せば そうなるはずですが）

で、私の解法は以下の通りです。

まず、材料の正方形は 3 つなので、一辺 √3 の正方形を 3等分するしかありません。

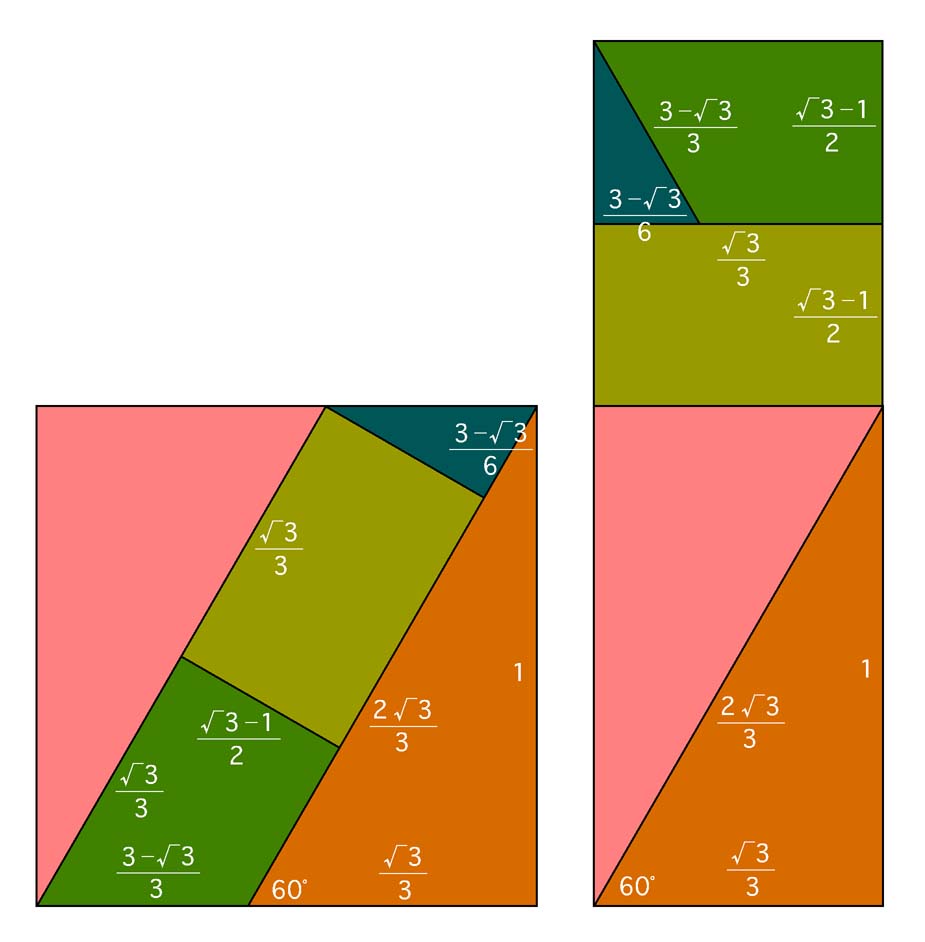
正方形を綺麗に 3等分するような対称形はなさそうなので、単純に縦に 3等分するしかないだろうと考えました。つまり、縦 √3 x 横 √3/3 の長方形を 3つ作ることにしました。

短辺の √3/3 は 1/√3 と書き換えられますので、一辺 1 の正方形の角から 60° の斜辺を降ろせば底辺が 1/√3 になります。

あとは適当に切って組み合わせれば、自動的に目的の長方形ができるはずです。念のため、数値を計算して ぴったり合うことを確認しました。

あとは、この長方形（上の図の右側）を横に3つ並べれば、一辺 √3 の正方形になります。

逆に言えば、一辺 √3 の正方形を3等分して3つの正方形を作りたいならば、縦に3当分しておいて、上の図の右側のように切って動かすと左のような一辺 1 の正方形が3つできることになります。

やはり数学の世界って美しいですね。
 

てことで、ではまた！

　　関連記事:

Objective-Cでの数値の丸め方：その2