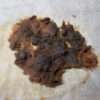
頭の体操：難しすぎると話題の小学4年生の算数問題、3つの正方形の面積の解法はいくつある？

こんばんは、数学大好きイワサキです。

Twitter で、小学4年生の算数の問題が難しすぎると話題になっていましたので、さっそく解いてみました。

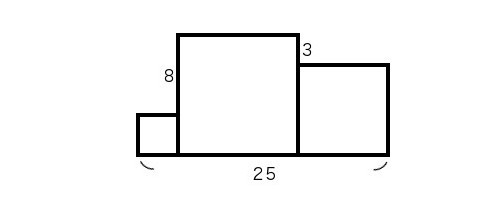
問題はこちら。

「3つの正方形の面積の和を求めましょう」

まだ答を見てない方はスクロールせずに、考えてみます？

　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
　　↓
 

解法

はい、では解法を書きます。

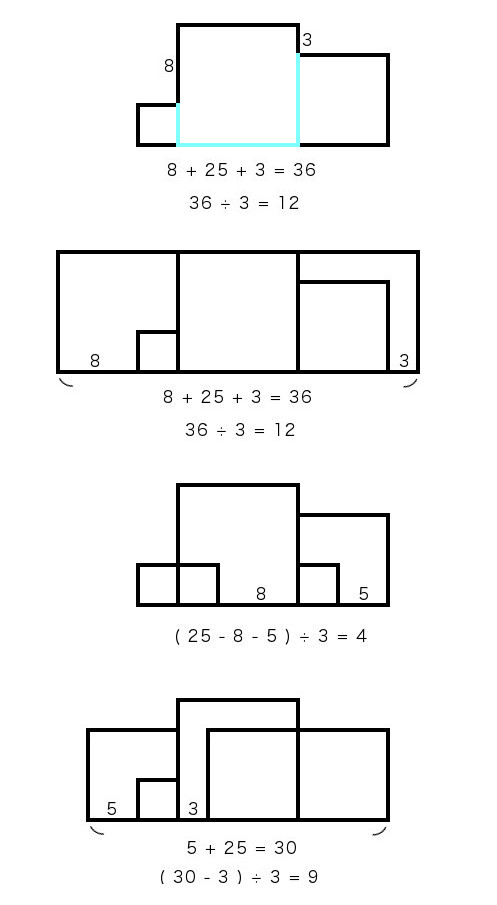
私が思いついたのは上の4つです。

一番上の折りたたむ方法が最も素直ですね。

二番目は一番の変形で、大を2つ追加。

三番目はちょっと変態っぽくて、小を追加。

四番目は変態確定で、中を追加する方法。
 

どれか一辺が分かれば、あとは2乗して面積の和を求めるだけです（省略ｗ）。
 

おまけ

小学4年生という縛りを無視して、方程式でも解いてみましょう。

大中小の正方形の一辺の長さをそれぞれ x, y, z と置くと、
x + y + z = 25
x – y = 3
x – z = 8
の連立方程式ができる

下2式を変形して
y = x – 3
z = x – 8

一番上の式に代入
x + ( x – 3 ) + ( x – 8 ) = 3 * x – 11 = 25
3 * x = 25 + 11 = 36
x = 36 / 3 = 12

結局、考え方は一番上の解法と同じなんですね。
　
 

解法はいくつある？

数学の問題を解くのは山登りと似ています。山頂に行けるルートは複数あります。この問題の場合も、少なくともメインルートだけで3つあります。派生ルートまで入れると、もっとたくさんあるはずです。

どれを選ぶか、「見通し」が悪くて間違ったルートを選ぶと山頂には行けませんが、どのルートを選ぶかという「見通し」の良さは、センスとしかいいようがありません。

この問題の場合、実直な小学生なら、問題文どおり一辺ではなく面積を求めようとして、迷路にハマるかもしれません。面積は難しそうだけど、一辺なら何とか求められそうだという見通しを持てるかどうかが最初のポイントでしょう。

あとは、大か小のどちらを作図で追加するかのセンスになると思いますが、個人的には小を追加するのが好きな私は変態なのでしょうか…
 

てことで、ではまた！

　　関連記事:

頭の体操：キッチンスケールなどの電子天びんで最大ひょう量より重いものを計る裏ワザ6つを図解