ボケ講座番外編2：ヒトの眼とカメラのボケ円径の比較

 
こんにちは、最近ボケ表現をあまり使っていない Iwasaki です。
 

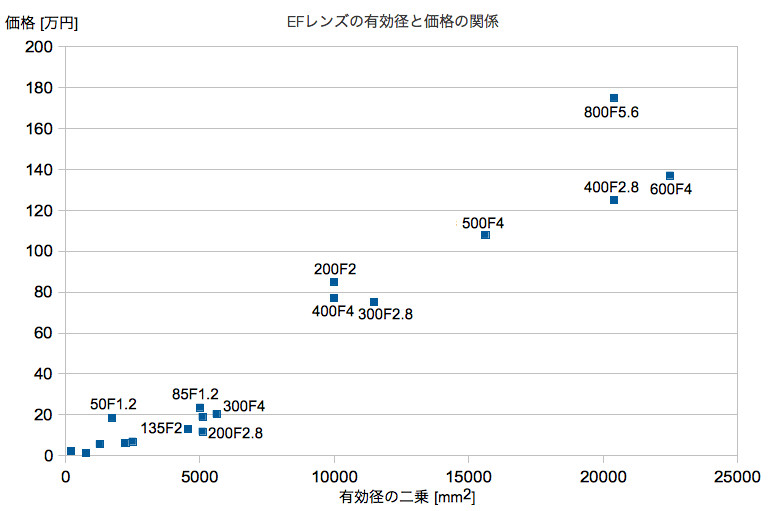
前回は、ボケ円径と被写界深度、ボケ円径とレンズ価格との関係について書きました。
ボケ円径が大きいほど被写界深度は浅く（ピントの合う範囲が狭く）、レンズ価格が高くなります。

今までボケ円径が大きいほどいいような書き方をして来ましたが、もちろんメリットもデメリットもあります。少し整理しておきましょう。フルサイズのイメージセンサーのメリットの記事と重なりますが。

【ボケ円径が大きいレンズのメリット】
・ボケ表現ができる。これは当然ですね。
・光量が多い。暗い所でも撮れたり、シャッタースピードを速くできたりします。感度をむやみに上げる必要もないので細かく見れば画質もいいです。
 

【ボケ円径が大きいレンズのデメリット】
・価格が高くなる。これは何度も述べました。
・レンズが大きく重くなる。携帯性が著しく低下しますね。
・被写界深度が浅くなる。ピント合わせがシビアになります。また、パンフォーカス表現のときに少し困ります。なぜ「少し」しか困らないかと言いますと、オートモードではなく絞り優先モードに切り替えて、意識的に絞り込めば解決できるからです。大は小を兼ねるというわけです。とはいえ、スナップや風景が多い場合、撮像板サイズの小さいカメラでオートで撮れば大抵ピントは合ってて楽チンではあります。
・収差が大きくなる。50mmF1.2と50mmF1.8のレンズをF2.8で使うと安くて小さい50mmF1.8の方が収差が少ないということは、しばしばあります。無理に大口径にすると収差の補正がとても難しくなるからです。
 

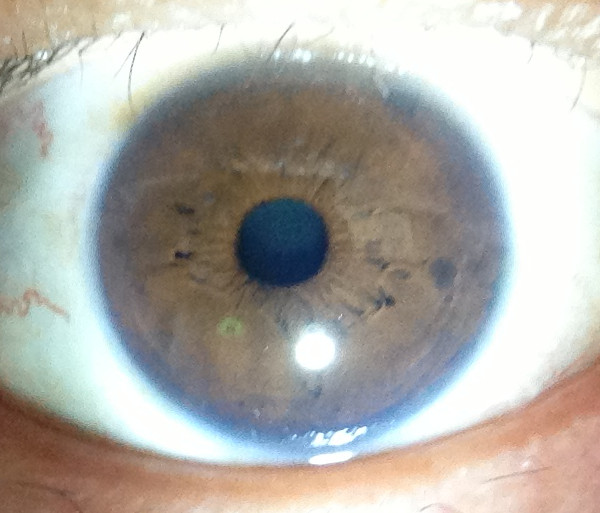
さて次に、カメラのお手本となるヒトの眼球（人眼）について考えてみましょう。

【ヒトの眼のボケ円径】
ヒトのボケ円径（有効径）は瞳孔径と同じです。

瞳孔径は、若い人の場合、暗所で8mmまで散瞳し、晴天の屋外で1〜2mmまで縮瞳します（対光反応）。また、近くの物を見るとき被写界深度が浅くなるのを補うために、縮瞳が起こります（近見反応）。しかし、残念ながらヒトの眼は、カメラのように意識的に散瞳・縮瞳をコントロールするこはできません。

明るすぎず暗すぎずの条件では、瞳孔径はだいたい 4mm 程度です。

人眼の焦点距離は約 17mm ですので、F値はおおむね F2〜F16、通常はF4ほどです。

ボケ円径が4mm程度のカメラの撮像板サイズ（フォーマット、センサーサイズ）はどの程度でしょうか？

ちょっと絞って F4 あたりでよく使うレンズの焦点距離は、4 x 4 = 16mm となります。焦点距離 16mm が標準レンズ（35mm判換算値で50mm程度）となるようなフォーマットの換算倍率は、50 ÷ 16 = 3 くらいです。

この記事を見返してみましょう。
　フルサイズのイメージセンサー（撮像素子、撮像板）のメリット その1：換算倍率とボケ円径

換算倍率が3に近いフォーマットは、1型の2.7かコンデジの5.6あたりですね。
多くのコンパクトデジタルカメラは、ヒトの眼と同等か、ややボケにくいレンズなんです。ピンボケの失敗が少ないことは、コンデジがフィルム時代のコンパクトカメラよりも普及した理由のひとつかもしれません。

フォーサーズ以上になると、ヒトの眼ではありえないほどのボケ円径（10mm以上）が使えるわけです。

こうして見ると、ボケ表現というのは、極めて不自然な絵ということになります。逆にいえば、ヒトの眼とは異次元の別世界だからこそ幻想的に感じるのでしょう。

ボケ表現を意識的に使いだしたのは、日本人の写真家だそうです。欧米人は数十年前までは、パンフォーカス表現が主体だったわけですね。

そう考えると、普段はお手軽にコンデジや iPhone でパンフォーカス、ここぞというとき、マクロやポートレートでボケ表現を使うという位でちょうどいいのかもしれませんね。
 

以上、カメラとヒトの眼をボケの観点から比較してみました。
 

てことで、ではまた！

　　関連記事:

デジカメを選ぶとき 何を基準にしたらいいの？ フルサイズのイメージセンサー（撮像素子、撮像板）のメリット その2：光量不足・拡大に強い ボケ講座番外編1：ボケ円径、被写界深度、レンズ価格の関係 サルには分からない、ボケの極意〜中級者編：ボケ円径の計算法 マニア向け ボケのすべて〜上級者編１：有限距離のボケ円径と前ボケの計算法 マニア向け ボケのすべて〜上級者編3：ボケ円径の実測とボケ味の評価